Interpretación Geométrica de las Soluciones de Sistemas de Ecuaciones: Guía Visual
En el ámbito de las matemáticas, la resolución de sistemas de ecuaciones es un proceso fundamental para la solución de problemas en diversas áreas, como la física, la economía y la informática. La interpretación geométrica de estas soluciones ofrece una perspectiva visual y intuitiva para comprender mejor la relación entre las variables involucradas. A través de esta guía visual, se presentará la forma en que las soluciones de sistemas de ecuaciones se pueden representar geométricamente, facilitando la comprensión y la aplicación práctica de estas herramientas matemáticas.

- Introducción a la Interpretación Geométrica de Soluciones de Sistemas de Ecuaciones
- ¿Qué es interpretar Geometricamente un sistema de ecuaciones?
- ¿Cómo están representadas geométricamente las soluciones de los sistemas de ecuaciones?
- ¿Qué significa interpretación geométrica?
- ¿Cómo se soluciona un sistema de ecuaciones por el metodo grafico?
- Solución de un sistema de ecuaciones por el método gráfico
- Mas informacion
- ¿Qué es la interpretación geométrica de las soluciones de sistemas de ecuaciones?
- ¿Cómo se representa un sistema de ecuaciones en un plano cartesiano?
- ¿Qué significan las intersecciones en la representación geométrica?
- ¿Cómo se puede utilizar la interpretación geométrica para resolver sistemas de ecuaciones?
Introducción a la Interpretación Geométrica de Soluciones de Sistemas de Ecuaciones
La interpretación geométrica de las soluciones de sistemas de ecuaciones es una herramienta fundamental en la resolución de problemas matemáticos y en la visualización de las relaciones entre variables. Esta guía visual te ayudará a entender mejor cómo las soluciones de sistemas de ecuaciones se representan geométricamente y cómo se utilizan estas representaciones para analizar y resolver problemas.
Definición de un Sistema de Ecuaciones
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que involucran a dos o más variables. Las ecuaciones en un sistema están relacionadas entre sí, y la resolución del sistema implica encontrar los valores de las variables que satisfacen todas las ecuaciones al mismo tiempo.
Representación Geométrica de un Sistema de Ecuaciones
En la representación geométrica de un sistema de ecuaciones, cada ecuación se representa como una recta o una curva en un plano cartesiano. Cada punto en la recta o curva representa una solución posible para la ecuación. Las soluciones del sistema de ecuaciones se encuentran en los puntos de intersección entre las rectas o curvas.
Intersección de Sucesos y Propiedades: Claves para Comprender EstadísticaTipos de Soluciones Geométricas
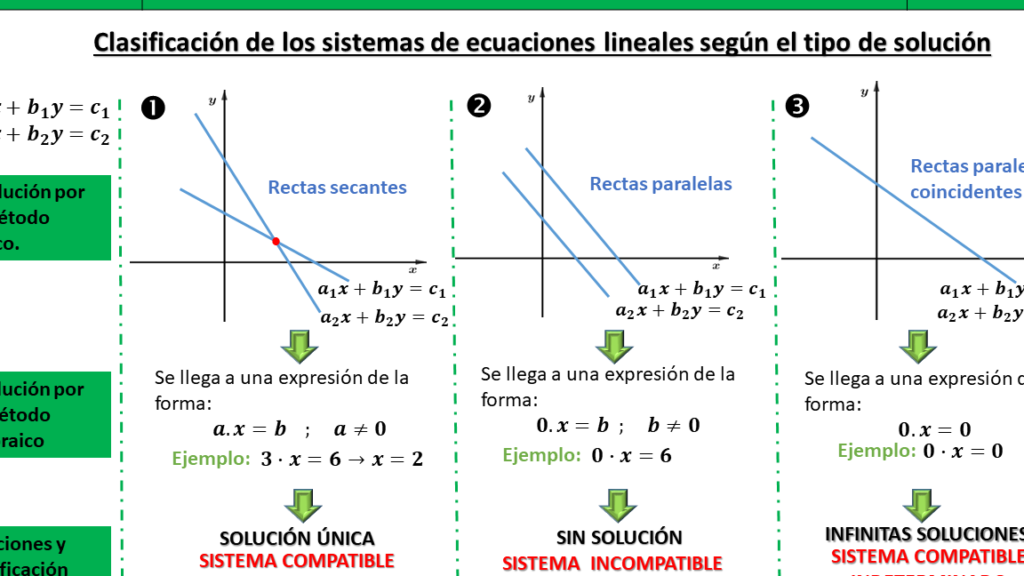
Existen varios tipos de soluciones geométricas para sistemas de ecuaciones, dependiendo de la relación entre las ecuaciones y las variables involucradas. Algunos de los tipos más comunes son: - Soluciones Únicas: Un sistema de ecuaciones con una solución única se representa geométricamente como el punto de intersección entre dos rectas no paralelas. - Soluciones Infinitas: Un sistema de ecuaciones con soluciones infinitas se representa geométricamente como dos rectas paralelas que nunca se intersectan. - No Soluciones: Un sistema de ecuaciones sin soluciones se representa geométricamente como dos rectas que se intersectan en un punto, pero no en el mismo plano cartesiano.
Importancia de la Interpretación Geométrica
La interpretación geométrica de las soluciones de sistemas de ecuaciones es importante porque permite visualizar y analizar las relaciones entre las variables involucradas. Esta visualización geométrica facilita la comprensión de los problemas y la identificación de las soluciones, lo que a su vez ayuda a resolver problemas más complejos en matemáticas y en otras disciplinas como la física, la economía y la ingeniería.
Aplicaciones Prácticas de la Interpretación Geométrica
La interpretación geométrica de las soluciones de sistemas de ecuaciones tiene numerosas aplicaciones prácticas en various campos. Algunos ejemplos incluyen: - Optimización: La interpretación geométrica se utiliza en la optimización para encontrar el máximo o mínimo de una función, representando las restricciones como rectas o curvas en un plano cartesiano. - Física: En la física, la interpretación geométrica se utiliza para modelar y analizar el movimiento de objetos y la relación entre fuerzas y velocidades. - Economía: En la economía, la interpretación geométrica se utiliza para analizar la relación entre variables económicas como la demanda y la oferta, y para determinar los equilibrios económicos.
| Tipo de Solución | Representación Geométrica |
|---|---|
| Solución Única | Intersección entre dos rectas no paralelas |
| Soluciones Infinitas | Rectas paralelas que nunca se intersectan |
| No Soluciones | Rectas que se intersectan en un punto, pero no en el mismo plano cartesiano |
¿Qué es interpretar Geometricamente un sistema de ecuaciones?

Introducción a la interpretación geométrica de sistemas de ecuaciones
La interpretación geométrica de un sistema de ecuaciones se basa en la representación gráfica de estas ecuaciones en un plano cartesiano. Cada ecuación del sistema se representa como una recta o curva en el plano, y el punto de intersección de estas rectas o curvas indica la solución del sistema. Esta forma de interpretar los sistemas de ecuaciones permite visualizar la relación entre las variables y facilita la comprensión de la solución.
Interpretación geométrica de un sistema de ecuaciones lineales
Un sistema de ecuaciones lineales se puede representar geométricamente como un conjunto de rectas en un plano cartesiano. Cada ecuación del sistema se representa como una recta, y la intersección de estas rectas indica la solución del sistema. Si las rectas se intersectan en un punto, el sistema tiene una solución única. Si las rectas son paralelas, el sistema no tiene solución. Y si las rectas coinciden, el sistema tiene infinitas soluciones.
- Solución única: Las rectas se intersectan en un punto.
- Sin solución: Las rectas son paralelas.
- Infinitas soluciones: Las rectas coinciden.
Interpretación geométrica de un sistema de ecuaciones no lineales
Un sistema de ecuaciones no lineales se puede representar geométricamente como un conjunto de curvas en un plano cartesiano. Cada ecuación del sistema se representa como una curva, y la intersección de estas curvas indica la solución del sistema. La interpretación geométrica de estos sistemas es más compleja que la de los sistemas lineales, ya que las curvas pueden tener más de un punto de intersección o no tener intersecciones.
- Curvas con intersecciones: Las curvas se intersectan en uno o más puntos.
- Curvas sin intersecciones: Las curvas no se intersectan.
- Curvas con infinitas intersecciones: Las curvas coinciden.
¿Cómo están representadas geométricamente las soluciones de los sistemas de ecuaciones?
Las soluciones de los sistemas de ecuaciones se representan geométricamente a través de la intersección de curvas o rectas en un gráfico. Cada ecuación en un sistema de ecuaciones se puede representar como una curva o recta en un gráfico, y las soluciones del sistema se encuentran en los puntos de intersección entre estas curvas o rectas. A continuación, se presentan algunos subtítulos y sus correspondientes detalles sobre cómo se representan geométricamente las soluciones de los sistemas de ecuaciones:
Rectas y Curvas
En un gráfico, las ecuaciones lineales se representan como rectas, mientras que las ecuaciones no lineales se representan como curvas. Las soluciones del sistema se encuentran en los puntos de intersección entre estas rectas y curvas. Por ejemplo, si se tiene un sistema de ecuaciones como:
2x + 3y = 7
x^2 + y^2 = 25
John Dewey: Aportaciones a la Filosofía Educativa y su ImpactoLa primera ecuación se representa como una recta y la segunda como una circunferencia. Las soluciones del sistema se encuentran en los puntos de intersección entre la recta y la circunferencia.
Intersección de Rectas
En el caso de sistemas de ecuaciones lineales, las soluciones se representan geométricamente como los puntos de intersección entre las rectas correspondientes a cada ecuación. Por ejemplo, si se tiene un sistema de ecuaciones como:
2x + 3y = 7
4x - 2y = 3
José de Espronceda: Descubre sus Obras más RelevantesLas soluciones del sistema se encuentran en los puntos de intersección entre estas dos rectas.
Intersección de Curvas
En el caso de sistemas de ecuaciones no lineales, las soluciones se representan geométricamente como los puntos de intersección entre las curvas correspondientes a cada ecuación. Por ejemplo, si se tiene un sistema de ecuaciones como:
x^2 + y^2 = 25
xy = 6
Las soluciones del sistema se encuentran en los puntos de intersección entre la circunferencia y la curva hiperbólica.
¿Qué significa interpretación geométrica?

La interpretación geométrica se refiere a la comprensión y análisis de la relación entre las figuras geométricas y sus características, como tamaño, forma, posición y orientación en el espacio. Esta interpretación se basa en la identificación de patrones y relaciones entre estas figuras, lo que permite la resolución de problemas y la comprensión de conceptos más complejos en matemáticas, ciencia, tecnología, ingeniería y matemáticas (STEM).
Tipos de interpretación geométrica
Existen diferentes tipos de interpretación geométrica, dependiendo del contexto y el propósito del análisis:
- Interpretación visual: se basa en la observación y la visualización de las figuras geométricas para identificar sus características y relaciones.
- Interpretación analítica: utiliza técnicas matemáticas y algebraicas para analizar y describir las figuras geométricas.
- Interpretación espacial: se enfoca en la relación entre las figuras geométricas en el espacio tridimensional.
Importancia de la interpretación geométrica
La interpretación geométrica es fundamental en various campos, como:
- Matemáticas: permite la comprensión de conceptos como la geometría, la trigonometría y la topología.
- Arquitectura: se utiliza para diseñar y construir edificios y estructuras, considerando la forma, tamaño y posición de los elementos.
- Ingeniería: es esencial para la resolución de problemas en diseño, construcción y operación de sistemas y estructuras.
Desarrollo de la interpretación geométrica
La interpretación geométrica se puede desarrollar a través de:
- Educación: la enseñanza de conceptos geométricos y técnicas de interpretación en la escuela.
- Práctica: la aplicación de la interpretación geométrica en problemas y proyectos reales.
- Tecnología: el uso de herramientas como software de diseño asistido por computadora (CAD) y visualización en 3D.
¿Cómo se soluciona un sistema de ecuaciones por el metodo grafico?

Solución de un sistema de ecuaciones por el método gráfico
El método gráfico es una forma visual de resolver sistemas de ecuaciones lineales. Se basa en la representación gráfica de las ecuaciones y la identificación del punto de intersección entre las dos rectas, que representan las soluciones del sistema. A continuación, se presentan los pasos generales para resolver un sistema de ecuaciones lineales por el método gráfico:
1. Representación gráfica de las ecuaciones
Primero, se necesitan representar gráficamente las dos ecuaciones del sistema. Para hacer esto, se reescriben las ecuaciones en la forma de pendiente-intercepto (y = mx + b), donde m es la pendiente y b es el intercepto. Luego, se trazan las rectas correspondientes a estas ecuaciones en un plano cartesiano.
- Reescribir las ecuaciones en la forma y = mx + b.
- Trazar las rectas correspondientes a estas ecuaciones en un plano cartesiano.
2. Identificación del punto de intersección
Una vez que se han trazado las rectas, se identifica el punto en el que estas se cruzan. Este punto de intersección es la solución del sistema de ecuaciones.
- Identificar el punto en el que las rectas se cruzan.
- Este punto de intersección es la solución del sistema de ecuaciones.
3. Verificación de la solución
Para verificar que la solución gráfica es correcta, se puede reemplazar los valores del punto de intersección en ambas ecuaciones del sistema. Si las ecuaciones se satisfacen, entonces la solución gráfica es correcta.
- Reemplazar los valores del punto de intersección en ambas ecuaciones del sistema.
- Verificar que las ecuaciones se satisfacen.
Mas informacion
¿Qué es la interpretación geométrica de las soluciones de sistemas de ecuaciones?
La interpretación geométrica de las soluciones de sistemas de ecuaciones es una forma de visualizar y analizar las soluciones de un sistema de ecuaciones a través de la representación gráfica en un plano cartesiano. Esta representación permite visualizar la relación entre las variables y la interacción entre las ecuaciones del sistema. Al representar las ecuaciones como rectas o curvas en un plano, se puede observar fácilmente la intersección de estas, que representan las soluciones del sistema. Esta forma de interpretación geométrica es fundamental en la resolución de sistemas de ecuaciones, ya que permite una visualización clara y fácil de entender de las soluciones.
¿Cómo se representa un sistema de ecuaciones en un plano cartesiano?
Un sistema de ecuaciones se representa en un plano cartesiano a través de la representación gráfica de cada ecuación como una recta o curva. Cada ecuación se representa en función de las variables x e y, y se traza en un plano cartesiano. Las ecuaciones se representan como rectas o curvas que se cruzan en uno o más puntos, que representan las soluciones del sistema. La representación geométrica permite visualizar fácilmente la relación entre las variables y la interacción entre las ecuaciones del sistema, facilitando la identificación de las soluciones.
¿Qué significan las intersecciones en la representación geométrica?
Las intersecciones en la representación geométrica de un sistema de ecuaciones representan las soluciones del sistema. Cada intersección entre las rectas o curvas que representan las ecuaciones indica un punto en el que se cumplen todas las ecuaciones del sistema. Estos puntos son las soluciones del sistema de ecuaciones, y representan los valores de las variables que satisfacen todas las ecuaciones. La cantidad y la posición de estas intersecciones dependen de las características del sistema de ecuaciones, y pueden variar desde un punto único hasta varias intersecciones o incluso no tener intersecciones.
¿Cómo se puede utilizar la interpretación geométrica para resolver sistemas de ecuaciones?
La interpretación geométrica se puede utilizar para resolver sistemas de ecuaciones a través de la visualización de las soluciones en un plano cartesiano. Al representar gráficamente las ecuaciones del sistema, se puede observar fácilmente la interacción entre estas y la relación entre las variables. Las intersecciones entre las rectas o curvas que representan las ecuaciones indican las soluciones del sistema. Esta forma de interpretación geométrica permite una visualización clara y fácil de entender de las soluciones, lo que facilita la resolución del sistema de ecuaciones. Además, esta representación geométrica puede ayudar a identificar sistemas inconsistentes o dependientes, que no tienen soluciones únicas o no tienen soluciones.
Si quieres conocer otros artículos parecidos a Interpretación Geométrica de las Soluciones de Sistemas de Ecuaciones: Guía Visual puedes visitar la categoría Arte y Música.

Entradas relacionadas