Intersección de Sucesos y Propiedades: Claves para Comprender Estadística
La estadística, como disciplina, se basa en la recolección y análisis de datos para extraer conclusiones significativas. La intersección de sucesos y propiedades es un concepto fundamental en este contexto, ya que permite entender la relación entre eventos y características en un conjunto de datos. Al comprender la interacción entre estas dos variables, los estadísticos pueden identificar patrones y tendencias, lo cual es crucial en campos como la investigación, la toma de decisiones y la predicción de eventos futuros. Esta interacción es clave para entender la estadística y su aplicación en la vida real.

- Intersección de Sucesos y Propiedades: Claves para Comprender Estadística
- ¿Qué es la intersección en estadistica?
- ¿Cómo saber la intersección de dos sucesos?
- ¿Qué es unión de sucesos en estadistica?
- Unión de sucesos en estadística
- ¿Cómo saber cuándo es unión o intersección en probabilidad?
- Mas informacion
Intersección de Sucesos y Propiedades: Claves para Comprender Estadística
La intersección de sucesos y propiedades es un concepto fundamental en estadística que permite analizar y comprender la relación entre diferentes eventos y características. En este sentido, la estadística se basa en la recolección y análisis de datos para inferir conclusiones sobre una población o un fenómeno en particular.
Definición de Sucesos y Propiedades
En estadística, un suceso se define como un evento o situación que puede ocurrir en un experimento o estudio. Por su parte, las propiedades se refieren a las características o atributos de los sucesos o poblaciones estudiadas. La interacción entre sucesos y propiedades es clave para entender la estadística y sus aplicaciones prácticas.
Tipos de Sucesos
Los sucesos en estadística se clasifican en dos categorías principales: sucesos elementales y sucesos compuestos. Los sucesos elementales son aquellos que no se pueden dividir en eventos más simples, mientras que los sucesos compuestos se componen de varios sucesos elementales.
Jerarquía de Operaciones Combinadas: Cómo Resolver Problemas MatemáticosTipos de Propiedades
Las propiedades en estadística se clasifican en dos tipos principales: propiedades cualitativas y propiedades cuantitativas. Las propiedades cualitativas se refieren a características no medibles, como el color o la forma, mientras que las propiedades cuantitativas se basan en medidas numéricas, como la altura o el peso.
Interacción entre Sucesos y Propiedades
La interacción entre sucesos y propiedades es fundamental para la estadística, ya que permite analizar la relación entre ellos y hacer inferencias sobre la población o fenómeno estudiado. Por ejemplo, si se está estudiando la relación entre la edad y la preferencia por cierto producto, la edad sería una propiedad cuantitativa y la preferencia por el producto sería una propiedad cualitativa. El suceso en este caso sería la compra del producto.
Aplicaciones Prácticas
La intersección de sucesos y propiedades tiene amplias aplicaciones prácticas en various campos, como la investigación de mercados, la epidemiología y la investigación social. En la investigación de mercados, por ejemplo, se analiza la relación entre las características demográficas de los consumidores (propiedades) y sus preferencias y comportamientos de compra (sucesos). En la epidemiología, se estudia la relación entre factores de riesgo (propiedades) y la incidencia de enfermedades (sucesos).
| Sucesos | Propiedades | Interacción |
|---|---|---|
| Comprar un producto | Edad, género, ingresos | Relación entre características demográficas y preferencias de compra |
| Contraer una enfermedad | Edad, género, hábitos de vida | Relación entre factores de riesgo y la incidencia de la enfermedad |
¿Qué es la intersección en estadistica?

Introducción a la intersección en estadística
La intersección en estadística se refiere al punto o puntos en los que dos o más conjuntos de datos se cruzan. Esta concepto es fundamental en la estadística y la teoría de la probabilidad, ya que permite analizar la relación entre diferentes variables y conjuntos de datos.
Tipos de intersección
Existen dos tipos principales de intersección:
- Intersección de conjuntos: Esta se refiere a la interacción entre dos conjuntos de datos, en la que los elementos de uno de los conjuntos también pertenecen al otro conjunto.
- Intersección de eventos: Esta se refiere a la interacción entre dos eventos, en la que la ocurrencia de uno de los eventos implica la ocurrencia del otro evento.
Importancia de la intersección en estadística
La intersección en estadística es importante por varias razones:
- Relación entre variables: La intersección permite analizar la relación entre variables y conjuntos de datos, lo que es fundamental en la investigación y el análisis estadístico.
- Teoría de la probabilidad: La intersección es un concepto clave en la teoría de la probabilidad, ya que permite calcular la probabilidad de que dos eventos ocurran al mismo tiempo.
- Análisis de datos: La intersección es una herramienta valiosa para el análisis de datos, ya que permite identificar patrones y relaciones entre conjuntos de datos.
¿Cómo saber la intersección de dos sucesos?

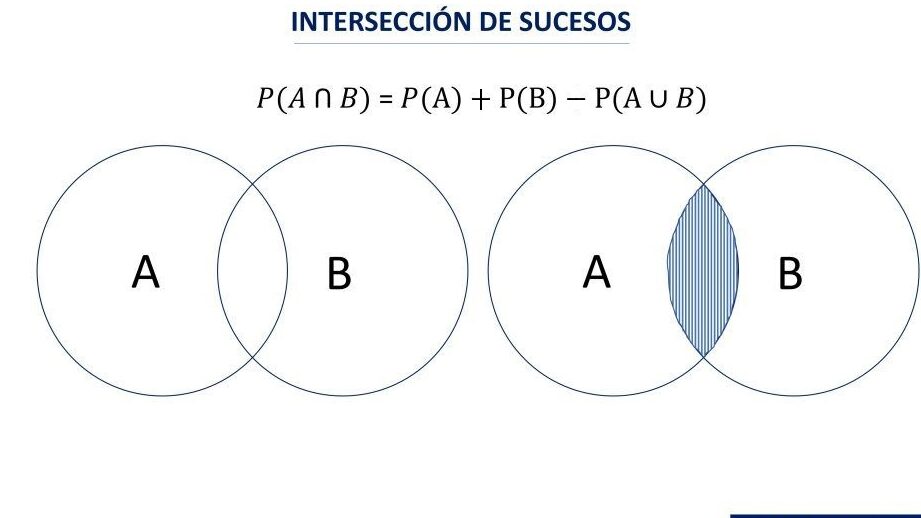
La intersección de dos sucesos se define como el conjunto de todos los elementos que pertenecen a ambos sucesos. En estadística y teoría de la probabilidad, la intersección de dos sucesos se denota como A ∩ B, y se lee como A intersección B. Esta sección te ayudará a entender cómo se calcula y qué implicaciones tiene en la teoría de la probabilidad.
Definición de intersección
La intersección de dos sucesos A y B es el conjunto de todos los elementos que pertenecen a ambos conjuntos. En otras palabras, es el conjunto de todos los elementos que se encuentran en A y, al mismo tiempo, en B. La intersección se denota como A ∩ B y se lee como A intersección B.
Cómo calcular la intersección
Para calcular la intersección de dos sucesos, necesitamos seguir los siguientes pasos:
- Identificar los conjuntos A y B.
- Encontrar los elementos que pertenecen a ambos conjuntos.
- La intersección de A y B es el conjunto de todos los elementos encontrados en el paso anterior.
Por ejemplo, si A = {1, 2, 3, 4} y B = {3, 4, 5, 6}, la intersección de A y B es {3, 4}.
Juglares y Trovadores: Diferencias Clave en la Literatura MedievalIntersección y probabilidad
En la teoría de la probabilidad, la intersección de dos sucesos es fundamental para calcular la probabilidad de que ambos sucesos ocurran al mismo tiempo. La probabilidad de la intersección de A y B se denota como P(A ∩ B) y se calcula como:
Probabilidad de la intersección: P(A ∩ B) = P(A) P(B), si A y B son sucesos independientes.
Es importante destacar que esta fórmula solo se aplica si los sucesos A y B son independientes. Si no lo son, se utilizan otras técnicas para calcular la probabilidad.
En resumen, la intersección de dos sucesos es un concepto fundamental en la teoría de la probabilidad que nos permite calcular la probabilidad de que ambos sucesos ocurran al mismo tiempo. Esta información es crucial para la toma de decisiones y la predicción de eventos futuros.
Kant Simplificado: Resumen de su Profundo Pensamiento Filosófico¿Qué es unión de sucesos en estadistica?

Unión de sucesos en estadística
En estadística, la unión de sucesos se refiere a la probabilidad de que al menos uno de los sucesos en un conjunto de sucesos mutuamente excluyentes ocurra. Esta probabilidad se calcula sumando las probabilidades de cada suceso individual.
Definición y notación
La unión de sucesos se denota con la letra U y se define como el conjunto de todos los resultados que pertenecen a al menos uno de los sucesos en cuestión. Por ejemplo, si A y B son dos sucesos, la unión de A y B se denota como A ∪ B.
- La unión de sucesos se basa en la probabilidad de que al menos uno de ellos ocurra.
- Se utiliza la notación A ∪ B para representar la unión de los sucesos A y B.
- La unión de sucesos es fundamental en la teoría de la probabilidad.
Cálculo de la probabilidad de la unión
Para calcular la probabilidad de la unión de dos sucesos, se suman las probabilidades de cada suceso individual. Esta fórmula se conoce como la fórmula de la inclusión-exclusión.
- La fórmula de la inclusión-exclusión es P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
- Donde P(A) y P(B) son las probabilidades de que ocurran los sucesos A y B, respectivamente.
- Y P(A ∩ B) es la probabilidad de que ambos sucesos ocurran al mismo tiempo.
Ejemplos
Un ejemplo clásico de unión de sucesos es el lanzamiento de un dado. Si queremos calcular la probabilidad de que salga un número par o un número impar, se aplicaría la fórmula de la inclusión-exclusión.
- Primero, se calcula la probabilidad de que salga un número par, que es 1/2.
- Luego, se calcula la probabilidad de que salga un número impar, que también es 1/2.
- Finalmente, se resta la probabilidad de que salga un número par y un número impar al mismo tiempo, que es 0, ya que estos sucesos son mutuamente excluyentes.
¿Cómo saber cuándo es unión o intersección en probabilidad?

Definición de Unión y Intersección en Probabilidad
En la teoría de la probabilidad, la unión y la intersección son dos conceptos fundamentales para determinar la probabilidad de que ocurra al menos uno o todos los eventos de un conjunto de eventos. La unión de dos eventos se define como el evento compuesto por todos los resultados que pertenecen a cualquiera de los dos eventos, mientras que la intersección de dos eventos se define como el evento compuesto por todos los resultados que pertenecen a ambos eventos.
Identificar la Unión o Intersección
Para determinar si un problema de probabilidad implica la unión o la intersección de eventos, es importante analizar la pregunta y los eventos involucrados. Si la pregunta pregunta por la probabilidad de que al menos uno de los eventos ocurra, entonces se está hablando de la unión de los eventos. Por otro lado, si la pregunta pregunta por la probabilidad de que todos los eventos ocurran, entonces se está hablando de la intersección de los eventos.
- La unión se utiliza cuando se pregunta por la probabilidad de que al menos uno de los eventos ocurra.
- La intersección se utiliza cuando se pregunta por la probabilidad de que todos los eventos ocurran.
Ejemplos Prácticos
Un ejemplo práctico de unión sería: ¿Cuál es la probabilidad de que lance un 4 o un 6 al tirar un dado? En este caso, se está hablando de la unión de los eventos lanzar un 4 y lanzar un 6.
Un ejemplo práctico de intersección sería: ¿Cuál es la probabilidad de que lance un 4 y un 6 al tirar dos dados? En este caso, se está hablando de la intersección de los eventos lanzar un 4 y lanzar un 6.
- Ejemplo de unión: ¿Cuál es la probabilidad de que lance un 4 o un 6 al tirar un dado?
- Ejemplo de intersección: ¿Cuál es la probabilidad de que lance un 4 y un 6 al tirar dos dados?
Mas informacion
¿Qué es la intersección de sucesos en estadística?
La intersección de sucesos en estadística se refiere a la situación en la que dos o más eventos ocurren al mismo tiempo. Esta intersección se representa con la notación A ∩ B, que significa A y B. La probabilidad de que ambos eventos ocurran al mismo tiempo se calcula como la probabilidad de que ocurra A veces la probabilidad de que ocurra B, es decir, P(A ∩ B) = P(A) P(B). La intersección de sucesos es fundamental en la estadística para analizar la relación entre variables y predecir la probabilidad de que ocurran eventos simultáneos.
¿Cómo se calcula la probabilidad de la intersección de sucesos?
Para calcular la probabilidad de la intersección de sucesos, se utiliza la fórmula P(A ∩ B) = P(A) P(B), como se mencionó anteriormente. Esta fórmula se basa en la suposición de que los eventos A y B son independientes, lo que significa que la ocurrencia de uno no afecta la probabilidad de que ocurra el otro. Sin embargo, si los eventos no son independientes, se utiliza la fórmula P(A ∩ B) = P(A) P(B|A), que toma en cuenta la probabilidad condicional de que ocurra B dada la ocurrencia de A.
¿Qué es la intersección de propiedades en estadística?
La intersección de propiedades en estadística se refiere a la relación entre dos o más características o variables en un conjunto de datos. Esta intersección se analiza para determinar si hay una relación significativa entre estas características, lo que puede ayudar a identificar patrones o tendencias en los datos. La intersección de propiedades se puede analizar utilizando técnicas como la correlación, que mide la relación entre dos variables, o la regresión, que permite predecir el valor de una variable basado en el valor de otra.
¿Por qué es importante la intersección de sucesos y propiedades en estadística?
La intersección de sucesos y propiedades es fundamental en estadística porque permite analizar y entender la relación entre variables y eventos. Al analizar la intersección de sucesos, los estadísticos pueden predecir la probabilidad de que ocurran eventos simultáneos, lo que es crucial en campos como la finanza, la medicina y la ingeniería. Por su parte, la intersección de propiedades permite identificar patrones y tendencias en los datos, lo que es esencial para la toma de decisiones y la investigación. En resumen, la intersección de sucesos y propiedades es clave para la comprensión y el análisis de datos en estadística.
Si quieres conocer otros artículos parecidos a Intersección de Sucesos y Propiedades: Claves para Comprender Estadística puedes visitar la categoría Arte y Música.

Entradas relacionadas