Jerarquía de Operaciones con Fracciones: Guía Esencial para Resolverlas
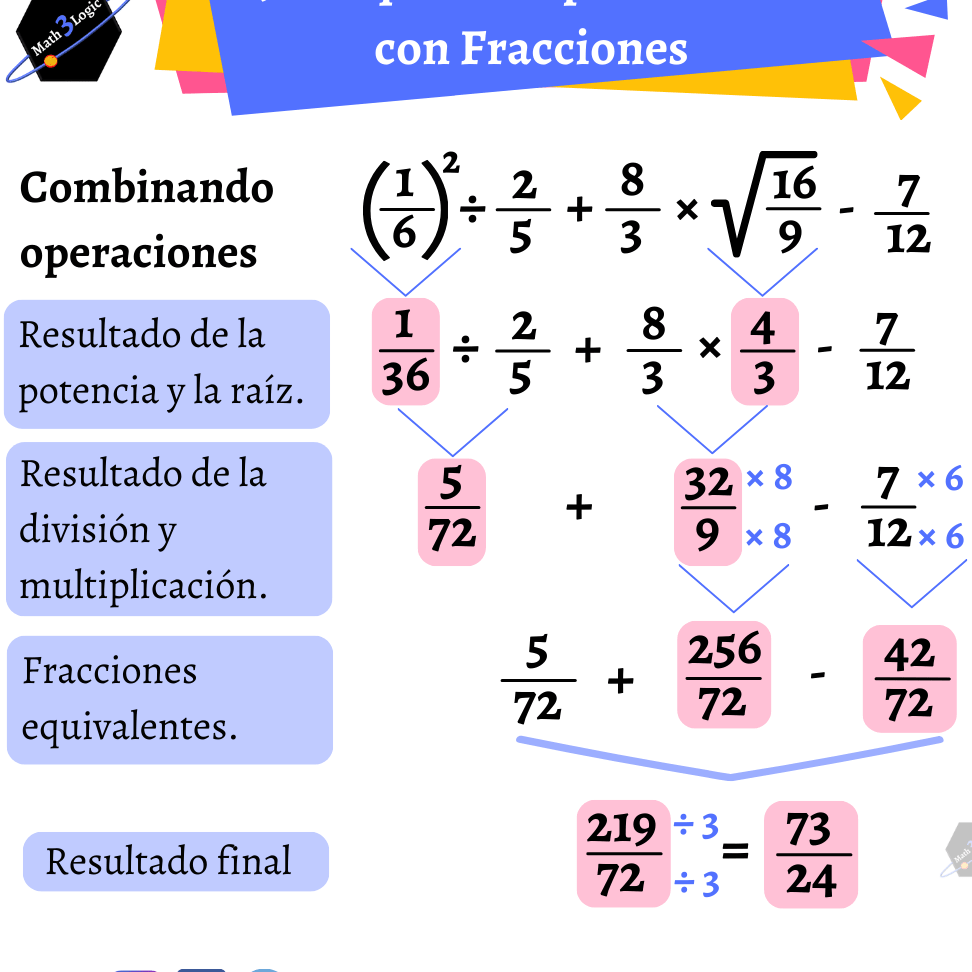
En el amplio y fascinante mundo de las matemáticas, las operaciones con fracciones son un concepto fundamental que ha brindado herramientas valiosas para resolver problemas en numerosas disciplinas. La jerarquía de estas operaciones es esencial para entender y aplicar adecuadamente las técnicas necesarias para solucionar ecuaciones y problemas que involucran fracciones. Esta guía esencial se centrará en la jerarquía de operaciones con fracciones, brindando a los lectores una comprensión clara y concisa de cómo resolver estas operaciones de manera correcta y eficiente.

- Jerarquía de Operaciones con Fracciones: Guía Esencial para Resolverlas
- ¿Cuál es la jerarquía de las fracciones?
- ¿Cuál es el orden para resolver fracciones?
- ¿Cómo se resuelve la jerarquía de operaciones paso a paso?
- ¿Cómo se realizan las operaciones básicas con las fracciones?
- Operaciones Básicas con Fracciones
- Mas informacion
Jerarquía de Operaciones con Fracciones: Guía Esencial para Resolverlas
La jerarquía de operaciones con fracciones es una herramienta fundamental para resolver expresiones matemáticas que involucran a estas. A continuación, te presentamos una guía esencial para comprender y aplicar esta jerarquía.
Introducción a la Jerarquía de Operaciones
La jerarquía de operaciones se basa en un orden establecido para realizar las operaciones matemáticas, evitando confusiones y garantizando que las expresiones se resuelvan de manera correcta. Esta jerarquía se aplica a todas las operaciones, incluyendo las que involucran fracciones.
La Jerarquía de Operaciones: PEMDAS/BODMAS
PEMDAS/BODMAS es un acrónimo que indica el orden en que se deben realizar las operaciones matemáticas. Esta jerarquía se aplica en la siguiente forma: - Parenthesis/Brackets (Paréntesis/Corchetes): Las operaciones dentro de paréntesis o corchetes se realizan primero. - Exponentiation/Orders (Exponentes/Órdenes): Las operaciones de exponentes o órdenes se realizan en segundo lugar. - Multiplication and Division (Multiplicación y División): Las operaciones de multiplicación y división se realizan en tercer lugar, de izquierda a derecha. - Addition and Subtraction (Adición y Sustracción): Las operaciones de adición y sustracción se realizan en último lugar, de izquierda a derecha.
Joan Miró: Esculturas Más Importantes y su Significado ArtísticoAplicación de la Jerarquía de Operaciones con Fracciones
Para aplicar la jerarquía de operaciones con fracciones, debes seguir el mismo orden establecido por PEMDAS/BODMAS. Primero, se resuelven las operaciones dentro de paréntesis o corchetes, luego las de exponentes o órdenes, seguidas de las operaciones de multiplicación y división, y finalmente las de adición y sustracción.
Ejemplos de Resolución de Expresiones con Fracciones
A continuación, te presentamos algunos ejemplos de resolución de expresiones con fracciones aplicando la jerarquía de operaciones: - Expresión: ( frac{3}{4} + frac{1}{2} times frac{5}{6} - frac{2}{3} ) - Resolución: Primero, se resuelve la multiplicación ( frac{1}{2} times frac{5}{6} = frac{5}{12} ). Luego, se suman las fracciones ( frac{3}{4} + frac{5}{12} = frac{9}{12} + frac{5}{12} = frac{14}{12} ). Finalmente, se resta la fracción ( frac{2}{3} ) del resultado anterior ( frac{14}{12} - frac{2}{3} = frac{14}{12} - frac{8}{12} = frac{6}{12} = frac{1}{2} ). - Expresión: ( frac{2}{3} div frac{4}{5} - frac{1}{2} + frac{3}{4} ) - Resolución: Primero, se resuelve la división ( frac{2}{3} div frac{4}{5} = frac{2}{3} times frac{5}{4} = frac{10}{12} ). Luego, se resta la fracción ( frac{1}{2} ) del resultado anterior ( frac{10}{12} - frac{6}{12} = frac{4}{12} ). Finalmente, se suma la fracción ( frac{3}{4} ) al resultado anterior ( frac{4}{12} + frac{9}{12} = frac{13}{12} ).
Importancia de la Jerarquía de Operaciones
La jerarquía de operaciones es fundamental para resolver expresiones matemáticas de manera correcta, especialmente cuando se involucran fracciones. Esta jerarquía garantiza que las operaciones se realicen en el orden adecuado, evitando confusiones y errores en los cálculos.
| Operación | Jerarquía |
|---|---|
| Paréntesis/Corchetes | Primero |
| Exponentes/Órdenes | Segundo |
| Multiplicación y División | Tercero |
| Adición y Sustracción | Cuarto |
¿Cuál es la jerarquía de las fracciones?

Las fracciones son una forma de representar cantidades parciales o divisiones de un todo. En matemáticas, las fracciones se utilizan para representar la relación entre dos cantidades. La jerarquía de las fracciones se establece en función de sus características y propiedades, que se clasifican en los siguientes niveles:
Fracciones Propias
Las fracciones propias son aquellas en las que el numerador (la parte superior) es menor que el denominador (la parte inferior). Por ejemplo, 1/2, 2/3, 3/4, etc. Estas fracciones representan cantidades parciales del todo.
- 1/2: La mitad del todo.
- 2/3: Dos tercios del todo.
- 3/4: Tres cuartos del todo.
Fracciones Impropias
Las fracciones impropias son aquellas en las que el numerador es mayor o igual que el denominador. Por ejemplo, 3/2, 4/3, 5/4, etc. Estas fracciones representan cantidades que son iguales o superan al todo.
- 3/2: Un todo y medio.
- 4/3: Un todo y un tercio.
- 5/4: Un todo y un cuarto.
Fracciones Equivalentes
Las fracciones equivalentes son aquellas que representan la misma cantidad, pero con diferentes numeradores y denominadores. Por ejemplo, 1/2 y 2/4 son equivalentes, ya que representan la misma cantidad.
La Caída de Constantinopla: Resumen de un Evento Crucial- 1/2 y 2/4: Representan la mitad del todo.
- 3/6 y 5/10: Representan la misma cantidad.
- 7/14 y 9/18: Son equivalentes y representan la misma cantidad.
¿Cuál es el orden para resolver fracciones?

Introducción
Resolver fracciones es un proceso que se basa en seguir un orden determinado para simplificar y operar con estas expresiones matemáticas. En este sentido, es fundamental comprender que la resolución de fracciones se hace siguiendo ciertas reglas y pasos que garantizan la exactitud en los resultados.
1. Identificar la fracción
El primer paso al resolver una fracción es identificarla. Para ello, debemos determinar qué es el numerador (número de arriba) y qué es el denominador (número de abajo). La fracción se expresa como numerador/denominador. Por ejemplo, en la fracción 3/4, el 3 es el numerador y el 4 es el denominador.
- Identificar el numerador.
- Identificar el denominador.
2. Simplificar la fracción
Después de identificar la fracción, es importante simplificarla. La simplificación se hace dividiendo tanto el numerador como el denominador entre su mayor divisor común. Por ejemplo, si tenemos la fracción 6/8, el mayor divisor común es 2, por lo que simplificamos la fracción a 3/4.
La Celestina: Resumen Corto y Perfecto para Estudiar- Encontrar el mayor divisor común del numerador y el denominador.
- Dividir el numerador y el denominador entre el mayor divisor común.
3. Realizar operaciones con fracciones
Una vez que la fracción está simplificada, es posible realizar operaciones con ella. Las operaciones más comunes son la suma, resta, multiplicación y división. Cada una de estas operaciones tiene sus propias reglas y pasos para resolverlas.
- Suma: Sumar los numeradores y dejar el denominador común.
- Resta: Restar los numeradores y dejar el denominador común.
- Multiplicación: Multiplicar los numeradores y los denominadores.
- División: Invertir la segunda fracción y multiplicar.
¿Cómo se resuelve la jerarquía de operaciones paso a paso?

La jerarquía de operaciones es una regla fundamental en matemáticas que indica el orden en que se deben realizar las operaciones en una expresión. Esta regla se aplica para asegurar que las operaciones se realicen de manera consistente y precisa. A continuación, se presentan los pasos para resolver la jerarquía de operaciones:
1. Identificar las operaciones
En primer lugar, es importante identificar las operaciones presentes en la expresión. Las operaciones principales son:
La Ciudad y los Perros: Personajes Claves y su Papel en la Novela- Paréntesis
- Exponentes
- Multiplicación y División
- Suma y Resta
Es importante destacar que estas operaciones se han clasificado en un orden jerárquico, es decir, se han asignado prioridades. Primero se resuelven los paréntesis, luego los exponentes, seguidos de la multiplicación y división, y finalmente la suma y resta.
2. Realizar las operaciones
Después de identificar las operaciones, se procede a resolverlas en el orden establecido:
Primero, se resuelven los paréntesis, es decir, se evalúan las expresiones dentro de ellos y se reemplazan por sus valores.
Luego, se resuelven los exponentes, es decir, se calculan las potencias.
Después, se resuelven las operaciones de multiplicación y división, en el orden en que se presentan de izquierda a derecha.
Por último, se resuelven las operaciones de suma y resta, también en el orden en que se presentan de izquierda a derecha.
3. Ejemplo
Para ilustrar mejor la aplicación de esta jerarquía, considera la siguiente expresión:
3 × 2 + 12 / 4 - 5 + 8^2
Primero, se resuelve el exponente:
3 × 2 + 12 / 4 - 5 + 64
Luego, se resuelven los paréntesis:
3 × 2 + 12 / 4 - 5 + 64
Después, se resuelven las operaciones de multiplicación y división:
6 + 3 - 5 + 64
Finalmente, se resuelven las operaciones de suma y resta:
6 + 3 - 5 + 64 = 68
¿Cómo se realizan las operaciones básicas con las fracciones?

Operaciones Básicas con Fracciones
Las fracciones son una forma de representar cantidades parciales o divisiones de un todo. Las operaciones básicas con fracciones, como la suma, resta, multiplicación y división, se utilizan para resolver problemas y expresar cantidades en forma de fracciones. A continuación, se presentan los detalles sobre cómo se realizan estas operaciones.
Suma de Fracciones
Para sumar fracciones, se deben seguir los siguientes pasos:
- Denominadores Comunes: Primero, se necesita encontrar el menor común denominador (MCD) entre los denominadores de las fracciones que se van a sumar. Esto se hace para que las fracciones tengan la misma base y puedan ser sumadas.
- Suma de Numeradores: Luego, se suman los numeradores de las fracciones y se divide entre el denominador común.
- Simplificación: Por último, se simplifica la fracción resultante, dividiendo tanto el numerador como el denominador entre su máximo común divisor.
Resta de Fracciones
Para restar fracciones, se siguen los mismos pasos que para sumar, con la excepción de que se resta el numerador de la segunda fracción del numerador de la primera:
- Denominadores Comunes: Primero, se necesita encontrar el menor común denominador (MCD) entre los denominadores de las fracciones que se van a restar.
- Resta de Numeradores: Luego, se resta el numerador de la segunda fracción del numerador de la primera y se divide entre el denominador común.
- Simplificación: Por último, se simplifica la fracción resultante, dividiendo tanto el numerador como el denominador entre su máximo común divisor.
Multiplicación y División de Fracciones
Para multiplicar y dividir fracciones, se utilizan las siguientes reglas:
- Multiplicación: Para multiplicar fracciones, se multiplican los numeradores y se multiplican los denominadores.
- División: Para dividir fracciones, se invierte la segunda fracción (cambiando el lugar del numerador y el denominador) y luego se multiplica.
- Simplificación: Después de multiplicar o dividir, se simplifica la fracción resultante, dividiendo tanto el numerador como el denominador entre su máximo común divisor.
Mas informacion
¿Qué es la jerarquía de operaciones con fracciones?
La jerarquía de operaciones con fracciones se refiere a un conjunto de reglas que se utilizan para determinar el orden en que se deben realizar las operaciones en una expresión matemática que involucra fracciones. Esta jerarquía es fundamental para asegurar que las operaciones se realicen de manera correcta y evitar confusiones o errores en los cálculos. Las operaciones se dividen en dos categorías principales: operaciones con números enteros y operaciones con fracciones. Dentro de estas categorías, existen subcategorías que establecen un orden preciso para la resolución de las operaciones.
¿Cómo se aplican las reglas de la jerarquía de operaciones con fracciones?
Las reglas de la jerarquía de operaciones con fracciones se aplican siguiendo un orden específico. Primero, se realizan las operaciones entre paréntesis, si existen. Luego, se llevan a cabo las operaciones de exponentes y raíces, en orden de izquierda a derecha. A continuación, se efectúan las operaciones de multiplicación y división, también de izquierda a derecha. Por último, se realizan las operaciones de suma y resta, en el mismo orden. Esta jerarquía es crucial para garantizar que las operaciones se realicen de manera correcta y se eviten errores en los cálculos.
¿Cómo se simplifican las fracciones en la jerarquía de operaciones?
La simplificación de fracciones en la jerarquía de operaciones se logra identificando el máximo común divisor (MCD) entre el numerador y el denominador de la fracción. El MCD es el mayor número que puede dividir exactamente tanto al numerador como al denominador. Dividiendo tanto el numerador como el denominador entre el MCD, se obtiene una fracción simplificada. Esta simplificación es fundamental en la jerarquía de operaciones con fracciones, ya que permite reducir la complejidad de las expresiones y facilitar los cálculos.
¿Por qué es importante la jerarquía de operaciones con fracciones en matemáticas?
La jerarquía de operaciones con fracciones es fundamental en matemáticas porque establece un orden preciso para la resolución de expresiones matemáticas complejas. Esta jerarquía garantiza que las operaciones se realicen de manera correcta y se eviten errores en los cálculos. Al seguir estas reglas, los estudiantes y profesionales pueden resolver problemas matemáticos de manera eficiente y precisa, lo que es esencial en various campos como la física, la ingeniería, la economía y la estadística, entre otros. La jerarquía de operaciones con fracciones es una herramienta valiosa para aquellos que necesitan resolver problemas matemáticos complejos.
Si quieres conocer otros artículos parecidos a Jerarquía de Operaciones con Fracciones: Guía Esencial para Resolverlas puedes visitar la categoría Lenguaje y Gramática.

Entradas relacionadas