La Complejidad de Multiplicar un Vector por un Escalar

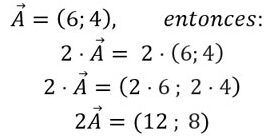
La complejidad de multiplicar un vector por un escalar es un concepto fundamental en el ámbito de la matemática y la física. Esta operación, aparentemente sencilla, implica la modificación de la magnitud del vector sin alterar su dirección. A pesar de su apariencia de simplicidad, esta operación es crucial en la resolución de problemas más complejos, como la determinación de la energía cinética o la comprensión del movimiento en la mecánica clásica. En este artículo, exploraremos a fondo la complejidad de esta operación y sus implicaciones en la resolución de problemas matemáticos y físicos.

La Complejidad de Multiplicar un Vector por un Escalar

La multiplicación de un vector por un escalar es una operación fundamental en matemáticas y física. Esta operación consiste en cambiar la magnitud del vector, sin alterar su dirección. Aunque parece simple, esta operación puede ser compleja dependiendo del contexto y las características del vector y del escalar.

Definición de Vector y Escalar

Un vector es una cantidad con magnitud y dirección, mientras que un escalar es una cantidad sin dirección. En la representación gráfica, los vectores se dibujan como flechas en un plano o espacio tridimensional, y los escalares se representan como números reales.

Operación de Multiplicación

La multiplicación de un vector por un escalar se define como la operación que cambiará la magnitud del vector, pero no su dirección. Si el escalar es positivo, la magnitud del vector aumentará; si es negativo, la magnitud disminuirá y el vector cambiará de dirección. La operación se representa matemáticamente como: V' = k V Donde V es el vector original, k es el escalar y V' es el vector resultante.

Complejidad en la Física

En la física, la multiplicación de un vector por un escalar se hace más compleja al considerar la relación entre la fuerza y la aceleración. Según la segunda ley de Newton, la fuerza aplicada a un objeto es igual a la masa del objeto multiplicada por su aceleración. Esta ley se puede representar matemáticamente como: F = m a Donde F es la fuerza, m es la masa y a es la aceleración. En este contexto, la masa actúa como un escalar y la aceleración como un vector. La complejidad surge al considerar la dirección de la fuerza y la aceleración, que deben ser la misma para que la ley se cumpla.

Complejidad en la Matemática

En la matemática, la complejidad de la multiplicación de un vector por un escalar se hace más evidente al considerar la teoría de espacios vectoriales. En este contexto, la multiplicación de un vector por un escalar se define como una operación lineal, es decir, que cumple con ciertas propiedades como la asociatividad y la distributividad. Esta teoría es fundamental en la resolución de sistemas de ecuaciones lineales y en la diagonalización de matrices.

Aplicaciones Prácticas

La multiplicación de un vector por un escalar tiene numerosas aplicaciones prácticas en diferentes campos. En la ingeniería, se utiliza para calcular la tensión en estructuras sometidas a cargas. En la física, se aplica para determinar la energía cinética de un objeto en movimiento. En la matemática, se utiliza en la resolución de sistemas de ecuaciones lineales y en la diagonalización de matrices.

Resumen

En resumen, la multiplicación de un vector por un escalar es una operación fundamental en matemáticas y física. Aunque parece simple, esta operación puede ser compleja dependiendo del contexto y las características del vector y del escalar. La complejidad surge al considerar la relación entre la fuerza y la aceleración en la física, y en la teoría de espacios vectoriales en la matemática. Las aplicaciones prácticas de esta operación son numerosas y variadas.

Mas informacion

¿Qué es la complejidad de multiplicar un vector por un escalar?

La complejidad de multiplicar un vector por un escalar se refiere al tiempo o espacio de memoria que se necesita para completar esta operación en un algoritmo o un programa de computadora. Esta operación es fundamental en la teoría de la complejidad computacional, que estudia los recursos necesarios para solucionar problemas en una computadora. En particular, la complejidad de multiplicar un vector por un escalar depende del tamaño del vector y del tipo de operaciones que se utilizan. Por lo general, se considera una operación simple y de baja complejidad, ya que solo implica la multiplicación de cada elemento del vector por un número constante. Sin embargo, en contextos más complejos, como la multiplicación de matrices o la resolución de sistemas de ecuaciones lineales, la complejidad puede aumentar significativamente.

¿Por qué es importante la complejidad de multiplicar un vector por un escalar en la teoría de la complejidad computacional?

La complejidad de multiplicar un vector por un escalar es importante en la teoría de la complejidad computacional porque se considera una de las operaciones más básicas y comunes en la resolución de problemas algorítmicos. Esta operación se utiliza en una gran variedad de contextos, como la resolución de sistemas de ecuaciones lineales, la multiplicación de matrices, la diagonalización de matrices y la resolución de problemas de optimización. La complejidad de esta operación se considera una base para la comprensión de la complejidad de otras operaciones más complejas. Por lo tanto, entender la complejidad de multiplicar un vector por un escalar es fundamental para analizar y diseñar algoritmos eficientes en términos de tiempo y espacio de memoria.

¿Cómo se calcula la complejidad de multiplicar un vector por un escalar?

La complejidad de multiplicar un vector por un escalar se calcula utilizando la notación de O (Big O), que indica el peor caso posible para la complejidad temporal o espacial de un algoritmo. En general, la complejidad de multiplicar un vector por un escalar es O(n), donde n es el tamaño del vector. Esto significa que el tiempo o espacio de memoria necesario para completar esta operación crece linealmente con el tamaño del vector. Sin embargo, esta complejidad puede variar dependiendo del contexto y del algoritmo utilizado. Por ejemplo, si se utilizan técnicas de multiplicación rápida o aritmética modular, la complejidad puede reducirse a O(log n) o O(sqrt(n)) en algunos casos.

¿Qué técnicas se utilizan para reducir la complejidad de multiplicar un vector por un escalar?

Para reducir la complejidad de multiplicar un vector por un escalar, existen varias técnicas que se utilizan comúnmente. Una de las técnicas más comunes es la multiplicación rápida, que permite reducir la complejidad a O(log n) utilizando técnicas de dividir y conquistar. Otra técnica es la aritmética modular, que se basa en la utilización de propiedades matemáticas específicas para reducir la complejidad. También se utilizan técnicas de preprocesamiento, como la normalización del vector, para reducir la complejidad. Finalmente, la utilización de hardware especializado, como las Unidades de Procesamiento de Vectores (VPUs), puede reducir significativamente la complejidad temporal y espacial de esta operación.

Si quieres conocer otros artículos parecidos a La Complejidad de Multiplicar un Vector por un Escalar puedes visitar la categoría Lenguaje y Gramática.