La Ley de Hardy-Weinberg: Explicación Clara de esta Ley Fundamental
La Ley de Hardy-Weinberg es una herramienta fundamental en la genética poblacional, que describe la evolución de la frecuencia de los alelos en una población. Esta ley, nombrada en honor a sus descubridores, Godfrey Harold Hardy y Wilhelm Weinberg, establece que en ausencia de factores evolutivos, como la deriva genética, la selección natural o la endogamia, la frecuencia de los alelos en una población se mantiene constante. Esta ley ofrece una visión clara y sencilla sobre cómo las características genéticas se transmiten y evolucionan en las poblaciones, lo que la hace esencial para entender la diversidad genética y la evolución de las especies.
La Ley de Hardy-Weinberg: Explicación Clara de esta Ley Fundamental
La Ley de Hardy-Weinberg es una herramienta fundamental en la genética de poblaciones, que describe la forma en que se distribuyen los alelos y genotipos en una población que se encuentra en equilibrio genético. Esta ley fue desarrollada por los matemáticos Godfrey Harold Hardy y Wilhelm Weinberg a principios del siglo XX. A continuación, se presentará una explicación clara y detallada de esta ley fundamental.
Definición y Explicación
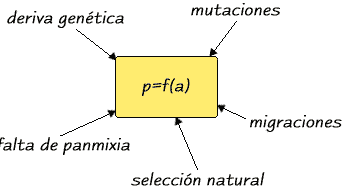
La Ley de Hardy-Weinberg establece que, en una población genéticamente equilibrada, la frecuencia de los alelos y genotipos se mantiene constante de una generación a otra. Esta ley se basa en ciertas condiciones, como la no existencia de mutaciones, la ausencia de deriva genética, la no selección natural, la panmixia (cruzamiento al azar) y la constancia del tamaño de la población.
Variables y Fórmulas
Para aplicar la Ley de Hardy-Weinberg, se utilizan las siguientes variables: - p: Frecuencia del alelo dominante - q: Frecuencia del alelo recesivo - p^2: Frecuencia del genotipo homocigoto dominante - 2pq: Frecuencia del genotipo heterocigoto - q^2: Frecuencia del genotipo homocigoto recesivo La fórmula principal de la Ley de Hardy-Weinberg es la siguiente: p^2 + 2pq + q^2 = 1
La Palabra: Significado y Significante Explicados de Manera ClaraAplicaciones y Ejemplos
La Ley de Hardy-Weinberg se aplica en various campos, como la genética de poblaciones, la evolución y la investigación en enfermedades genéticas. Un ejemplo de aplicación es el cálculo de la frecuencia de un genotipo o alelo en una población. Por ejemplo, si se sabe que la frecuencia del alelo dominante es del 60%, se puede calcular la frecuencia del alelo recesivo y los genotipos utilizando la fórmula principal.
Limitaciones y Críticas
Aunque la Ley de Hardy-Weinberg es una herramienta valiosa, tiene algunas limitaciones. No considera la deriva genética, la selección natural, las mutaciones y la no panmixia, lo cual puede afectar la precisión de los cálculos en poblaciones reales.
Importancia en la Genética Moderna
La Ley de Hardy-Weinberg sigue siendo fundamental en la genética moderna, ya que permite analizar la estructura genética de las poblaciones y entender la evolución de las especies. También es utilizada en la investigación de enfermedades genéticas para determinar la frecuencia de los alelos y genotipos asociados con estas enfermedades.
| Variable | Definición | Fórmula |
|---|---|---|
| p | Frecuencia del alelo dominante | p |
| q | Frecuencia del alelo recesivo | q |
| p^2 | Frecuencia del genotipo homocigoto dominante | p^2 |
| 2pq | Frecuencia del genotipo heterocigoto | 2pq |
| q^2 | Frecuencia del genotipo homocigoto recesivo | q^2 |
Mas informacion
¿Qué es la ley de Hardy-Weinberg?
La ley de Hardy-Weinberg es una herramienta fundamental en la genética poblacional que describe la relación entre las frecuencias alélicas y genotípicas en una población en equilibrio. Esta ley, propuesta por Godfrey Harold Hardy y Wilhelm Weinberg en 1908, establece que, en ausencia de factores evolutivos como la deriva genética, la selección natural y la flujo genético, las frecuencias alélicas y genotípicas en una población permanecen constantes de una generación a la siguiente. Esta ley se basa en ciertas suposiciones, como la panmixia (mezcla aleatoria de individuos), la ausencia de mutaciones y la no existencia de selección natural. La ley de Hardy-Weinberg es utilizada para analizar la genética de poblaciones y predecir la evolución de estas.
La Sílaba: Definición y Reglas para su Identificación¿Cómo se aplica la ley de Hardy-Weinberg?
La aplicación de la ley de Hardy-Weinberg implica seguir ciertos pasos. Primero, se identifican las frecuencias alélicas y genotípicas en una población. Luego, se verifica si se cumplen las suposiciones necesarias para aplicar la ley, como la panmixia y la ausencia de mutaciones. A continuación, se utilizan las fórmulas de Hardy-Weinberg para calcular las frecuencias alélicas y genotípicas esperadas en la siguiente generación. Estas fórmulas se basan en la relación entre la frecuencia de un alelo y la frecuencia del genotipo homocigoto correspondiente. Finalmente, se comparan las frecuencias observadas con las esperadas para determinar si la población está en equilibrio.
¿Qué son las suposiciones de la ley de Hardy-Weinberg?
Las suposiciones de la ley de Hardy-Weinberg son condiciones necesarias para que se cumplan las predicciones de esta ley. Estas suposiciones incluyen la panmixia, que implica la mezcla aleatoria de individuos en la población; la ausencia de mutaciones, que garantiza que no haya cambios en las frecuencias alélicas; la no existencia de selección natural, que significa que todos los genotipos tienen la misma probabilidad de sobrevivir y reproducirse; y la ausencia de flujo genético, que implica que no hay intercambio de genes con otras poblaciones. Estas suposiciones son idealizaciones, ya que en la realidad, estas condiciones no se cumplen siempre. Sin embargo, la ley de Hardy-Weinberg sigue siendo una herramienta útil para analizar la genética de poblaciones.
¿Qué implicaciones tiene la ley de Hardy-Weinberg en la genética?
La ley de Hardy-Weinberg tiene importantes implicaciones en la genética. Primero, permite analizar la genética de poblaciones y predecir la evolución de estas. Esta ley indica que, en ausencia de factores evolutivos, las frecuencias alélicas y genotípicas permanecen constantes. Esto significa que, si se conoce la frecuencia de un alelo en una población, se puede predecir la frecuencia del genotipo homocigoto correspondiente. La ley de Hardy-Weinberg también es fundamental en la identificación de desequilibrios genéticos, que pueden indicar la presencia de selección natural o flujo genético. En resumen, la ley de Hardy-Weinberg es una herramienta fundamental en la genética poblacional para analizar y predecir la evolución de las poblaciones.
La Tilde Diacrítica: Reglas y EjemplosSi quieres conocer otros artículos parecidos a La Ley de Hardy-Weinberg: Explicación Clara de esta Ley Fundamental puedes visitar la categoría Ciencia y Tecnología.

Entradas relacionadas