Las Posiciones Relativas de Dos Rectas en el Plano: Un Análisis
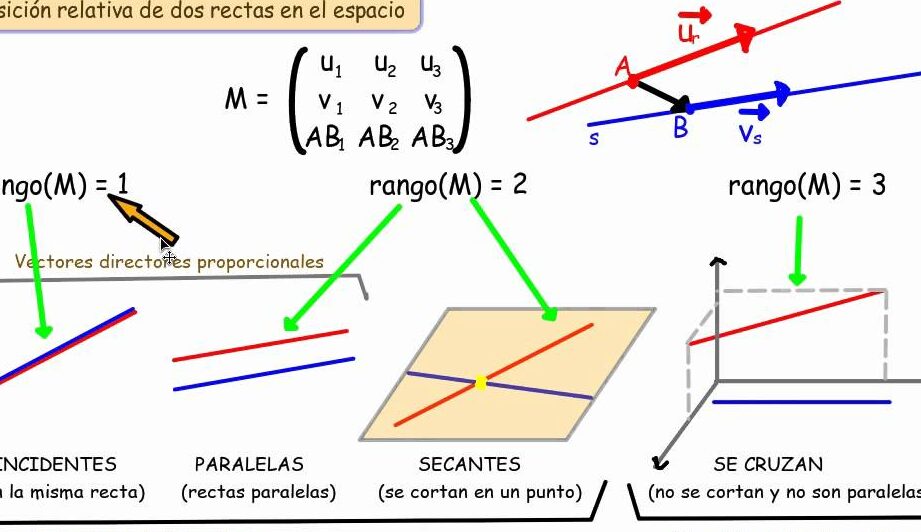
En el ámbito de la geometría plana, las posiciones relativas de dos rectas son un tema fundamental para comprender y analizar la interacción entre estas figuras geométricas. Las rectas, como conceptos matemáticos, pueden estar en relación de paralelismo, perpendicularidad o ser secantes. Esta relación no solo determina la forma en que estas rectas se cruzan o no entre sí, sino que también influye en la formación de ángulos y figuras geométricas más complejas. En este artículo, se analizará en profundidad las posiciones relativas de dos rectas en el plano, destacando sus características y aplicaciones en la resolución de problemas geométricos.

- Las Posiciones Relativas de Dos Rectas en el Plano: Un Análisis
- ¿Cuáles son las posiciones relativas de dos rectas en el plano?
- ¿Cuáles son las posiciones relativas de dos planos?
- ¿Qué analiza la posición relativa?
- ¿Cómo se clasifican las rectas según su posición en el plano?
- Clasificación de las rectas en el plano
- Mas informacion
Las Posiciones Relativas de Dos Rectas en el Plano: Un Análisis
En matemáticas, especialmente en geometría, el estudio de las posiciones relativas de dos rectas en un plano es fundamental para comprender sus características y relaciones. Las rectas pueden estar en posición paralela, perpendicular o oblicua entre sí, lo que afecta la forma en que se cruzan y sus propiedades geométricas.
Rectas Paralelas
Dos rectas son paralelas si no se intersectan, sin importar cuánto se extiendan. Las rectas paralelas comparten la misma pendiente, lo que significa que sus pendientes son iguales. Por ejemplo, si una recta tiene una pendiente de 3, todas las rectas paralelas a ella también tendrán una pendiente de 3.
Rectas Perpendiculares
Dos rectas son perpendiculares si se cruzan formando un ángulo recto (90 grados). Las rectas perpendiculares tienen pendientes que son inversas y opuestas. Por ejemplo, si una recta tiene una pendiente de 4, todas las rectas perpendiculares a ella tendrán una pendiente de -1/4.
Lengua vs. Lenguaje: Semejanzas y DiferenciasRectas Oblicuas
Dos rectas son oblicuas si se cruzan en un ángulo distinto de 90 grados. Las rectas oblicuas no comparten la misma pendiente, ni son inversas y opuestas como las perpendiculares. En lugar de eso, sus pendientes se relacionan a través de la fórmula de la pendiente de la recta perpendicular, que es la inversa y opuesta de la pendiente original.
Intersección de Rectas
La intersección de dos rectas ocurre en un punto común entre ambas. Si las rectas son paralelas, no se intersectan. Si las rectas son perpendiculares o oblicuas, se intersectan en un punto. El punto de intersección puede ser determinado usando las ecuaciones de las rectas y resolviendo el sistema de ecuaciones resultante.
Aplicaciones en la Vida Real
El estudio de las posiciones relativas de dos rectas en un plano tiene numerosas aplicaciones en la vida real. Por ejemplo, en la arquitectura, la relación entre las paredes y el suelo es crucial para la estructura y la estabilidad del edificio. En la física, la trayectoria de un proyectil se puede modelar como la intersección de dos rectas, una para la trayectoria horizontal y otra para la vertical. En la ingeniería, la relación entre las rectas es fundamental para diseñar estructuras y sistemas que funcionen correctamente.
| Tipo de Posición | Características | Ejemplos |
|---|---|---|
| Paralela | Las rectas no se intersectan y comparten la misma pendiente. | Las vías del tren y la carretera. |
| Perpendicular | Las rectas se intersectan en un ángulo recto y sus pendientes son inversas y opuestas. | Los ejes x e y en un gráfico. |
| Oblicua | Las rectas se intersectan en un ángulo distinto de 90 grados y sus pendientes están relacionadas. | Los lados de un triángulo. |
¿Cuáles son las posiciones relativas de dos rectas en el plano?

Introducción
En geometría, las rectas son figuras geométricas que se extienden indefinidamente en dos direcciones. Las rectas en un plano se clasifican en relación con su posición relativa entre sí. A continuación, se presentan las posiciones relativas de dos rectas en un plano.
Rectas Paralelas
Las rectas paralelas son aquellas que, sin importar la distancia entre ellas, nunca se cruzan. En un plano, estas rectas tienen la misma pendiente y un punto de intersección en el infinito. Las rectas paralelas se representan con la notación AB // CD.
- Las rectas paralelas no se cruzan.
- Las rectas paralelas tienen la misma pendiente.
- Las rectas paralelas tienen un punto de intersección en el infinito.
Rectas Perpendiculares
Las rectas perpendiculares, también conocidas como rectas ortogonales, son aquellas que se cruzan en un ángulo recto (90 grados). En un plano, estas rectas tienen pendientes que se relacionan como opuestos recíprocos. Las rectas perpendiculares se representan con la notación AB ⊥ CD.
- Las rectas perpendiculares se cruzan en un ángulo recto.
- Las rectas perpendiculares tienen pendientes opuestas recíprocas.
- Las rectas perpendiculares se cruzan en un punto.
Rectas Secantes
Las rectas secantes son aquellas que se cruzan en un punto, pero no son perpendiculares. En un plano, estas rectas tienen pendientes diferentes y se cruzan en un punto determinado. Las rectas secantes se representan con la notación AB ∩ CD.
Ley del Acento Final: Ejemplos y Explicación- Las rectas secantes se cruzan en un punto.
- Las rectas secantes no son perpendiculares.
- Las rectas secantes tienen pendientes diferentes.
¿Cuáles son las posiciones relativas de dos planos?

Definición de planos
Los planos son superficies geométricas bidimensionales que no tienen espesor ni grosor. Estas superficies se utilizan para describir figuras geométricas y espacios en la geometría y la topología. En el contexto de la geometría, los planos se definen como conjuntos de puntos que se encuentran a la misma distancia de un punto fijo, denominado polo.
Posiciones relativas de dos planos
Los planos en un espacio tridimensional pueden tener varias posiciones relativas entre sí. A continuación, se presentan las principales posiciones relativas de dos planos:
- Paralelos: Dos planos se consideran paralelos si no se intersectan, es decir, no comparten puntos comunes.
- Perpendiculares: Dos planos se consideran perpendiculares si forman un ángulo recto entre ellos, es decir, 90 grados.
- Oblicuos: Dos planos se consideran oblicuos si no son paralelos ni perpendiculares entre sí, es decir, forman un ángulo agudo o obtuso.
Intersección de dos planos
La intersección de dos planos en un espacio tridimensional es una línea recta. Esta línea es común a ambos planos y los divide en dos semiplanos cada uno. La intersección de dos planos depende de sus posiciones relativas:
Lista Completa de Países de África y sus Capitales para Viajeros- Intersección de planos paralelos: No hay intersección entre dos planos paralelos, ya que no comparten puntos comunes.
- Intersección de planos perpendiculares: La intersección de dos planos perpendiculares es una línea recta que forma un ángulo recto con ambos planos.
- Intersección de planos oblicuos: La intersección de dos planos oblicuos es una línea recta que no forma un ángulo recto con ninguno de los planos.
¿Qué analiza la posición relativa?

La posición relativa se analiza en diferentes contextos y disciplinas. A continuación, se presentan tres subtítulos h3 relacionados con la posición relativa y sus análisis detallados:
1. Análisis de la posición relativa en astronomía
En astronomía, la posición relativa se analiza para determinar la ubicación de los objetos celestes entre sí y en relación con la Tierra. Esto se hace a través de técnicas como la astrometría, que mide la posición angular de los objetos en el cielo y su distancia a la Tierra. La posición relativa de los objetos celestes es fundamental para entender la estructura del universo y la dinámica de los sistemas planetarios.
- Astrometría: Mide la posición angular de los objetos en el cielo y su distancia a la Tierra.
- Paralaje: Es una técnica utilizada para medir la distancia de objetos cercanos a la Tierra.
- Spectroscopia: Permite analizar la composición y velocidad de los objetos celestes.
En la navegación, la posición relativa se analiza para determinar la ubicación de un objeto o persona en relación con otros objetos o referencias. Esto se hace a través de técnicas como la triangulación, que utiliza la medición de ángulos y distancias entre puntos de referencia conocidos para determinar la posición exacta de un objeto. La posición relativa es fundamental en la navegación para determinar la trayectoria adecuada y evitar colisiones.
Lista Completa de los Órganos Internos del Cuerpo Humano que Maravillan- Triangulación: Utiliza la medición de ángulos y distancias entre puntos de referencia conocidos.
- GPS: Utiliza señales de satélites para determinar la posición exacta de un objeto o persona.
- Radar: Utiliza ondas de radio para determinar la distancia y velocidad de un objeto.
3. Análisis de la posición relativa en la sociología
En sociología, la posición relativa se analiza para entender la relación entre los individuos o grupos en una sociedad. La posición relativa se determina por factores como la riqueza, el estatus social, la educación y la ocupación. La posición relativa es fundamental para entender la estructura social y las interacciones entre los miembros de una sociedad.
- Estatus social: La posición relativa se determina por el estatus social de los individuos o grupos.
- Riqueza: La riqueza es un factor importante en la determinación de la posición relativa.
- Educación: La educación también es un factor clave en la determinación de la posición relativa.
¿Cómo se clasifican las rectas según su posición en el plano?

Clasificación de las rectas en el plano
En geometría, las rectas se clasifican según su posición en el plano en paralelas, perpendiculares y oblicuas.
Rectas paralelas
Las rectas paralelas son aquellas que se encuentran en el mismo plano y nunca se intersectan, sin importar cuán lejos se extiendan.
- Se representan con la notación AB // CD.
- La distancia entre dos rectas paralelas es constante en todos los puntos.
- Los ángulos formados por dos rectas paralelas y una transversal son congruentes.
Rectas perpendiculares
Las rectas perpendiculares son aquellas que se intersectan formando un ángulo recto (90 grados).
- Se representan con la notación AB ⊥ CD.
- La intersección de dos rectas perpendiculares forma cuatro ángulos rectos.
- Las rectas perpendiculares son útiles en la resolución de problemas de trigonometría.
Rectas oblicuas
Las rectas oblicuas son aquellas que no son paralelas ni perpendiculares entre sí.
- Forman ángulos agudos o obtusos al intersectarse.
- La intersección de dos rectas oblicuas forma cuatro ángulos no rectos.
- Las rectas oblicuas se utilizan en la resolución de problemas que involucran triángulos no rectángulos.
Mas informacion
¿Qué son las posiciones relativas de dos rectas en el plano?
Las posiciones relativas de dos rectas en el plano se refieren a la relación entre estas rectas en un espacio bidimensional. Las rectas pueden estar en paralelo, es decir, no se intersectan, o pueden ser perpendiculares, formando un ángulo recto entre ellas. También es posible que las rectas se cruzan en un punto común. En este último caso, las rectas se llaman transversales. El estudio de estas posiciones relativas es fundamental en geometría y matemáticas, ya que permite analizar y resolver problemas geométricos y algebraicos de forma más eficiente.
¿Cómo se determina si dos rectas son paralelas?
Para determinar si dos rectas son paralelas, se utilizan técnicas geométricas y algebraicas. En geometría, si dos rectas no se intersectan y están en el mismo plano, se consideran paralelas. En álgebra, se puede analizar la pendiente de las rectas. Si las pendientes son iguales, las rectas son paralelas. Si las pendientes son diferentes, las rectas no son paralelas y pueden ser perpendiculares o transversales. En este sentido, la pendiente es una herramienta fundamental para analizar las posiciones relativas de las rectas.
¿Qué es una recta perpendicular?
Una recta perpendicular es aquella que forma un ángulo recto (90 grados) con otra recta. Las rectas perpendiculares se utilizan en geometría y matemáticas para resolver problemas que involucran ángulos rectos y figuras geométricas regulares, como cuadrados y rectángulos. Las rectas perpendiculares también se utilizan en la resolución de problemas de trigonometría y en la construcción de figuras geométricas complejas. La perpendicularidad es una propiedad fundamental en la geometría, ya que permite la creación de figuras geométricas regulares y la resolución de problemas que involucran ángulos rectos.
¿Por qué es importante el estudio de las posiciones relativas de las rectas?
El estudio de las posiciones relativas de las rectas es fundamental en geometría y matemáticas, ya que permite analizar y resolver problemas geométricos y algebraicos de forma más eficiente. Las rectas paralelas, perpendiculares y transversales se utilizan en la resolución de problemas que involucran figuras geométricas regulares y complejas, como triángulos, cuadriláteros, polígonos y circunferencias. La comprensión de estas posiciones relativas también es crucial en la trigonometría, la geometría analítica y la topología, y se aplica en campos como la arquitectura, la ingeniería y la ciencia.
Si quieres conocer otros artículos parecidos a Las Posiciones Relativas de Dos Rectas en el Plano: Un Análisis puedes visitar la categoría Lenguaje y Gramática.

Entradas relacionadas