Potencias de la Unidad Imaginaria: Conceptos que Ampliarán tu Mente
En el fascinante terreno de las matemáticas, existen conceptos que amplían nuestra comprensión y nos permiten explorar nuevas dimensiones. Las potencias de la unidad imaginaria son uno de ellos. Esta te guiará a través de un viaje intelectual en el que descubrirás la belleza y la complejidad de estas potencias, cómo se utilizan en la resolución de ecuaciones y la representación de funciones periódicas, y cómo amplían nuestra visión del mundo. Preparen sus mentes para un viaje a través del tiempo y el espacio, donde la imaginación y la matemática se unen en un baile celestial.
- Explorando las Potencias de la Unidad Imaginaria: Un Viaje hacia la Ampliación de la Mente
- Mas informacion
- ¿Qué son las potencias de la unidad imaginaria?
- ¿Cómo se utilizan las potencias de la unidad imaginaria en la teoría de Galois?
- ¿Qué relación hay entre las potencias de la unidad imaginaria y la resolución de ecuaciones algebraicas?
- ¿Cómo se aplican las potencias de la unidad imaginaria en la teoría de la representación de grupos?
Explorando las Potencias de la Unidad Imaginaria: Un Viaje hacia la Ampliación de la Mente
La Unidad Imaginaria es un concepto matemático que ha revolucionado la forma en que se abordan los problemas en álgebras y análisis complejos. A través de la exploración de estas potencias, los estudiantes y profesionales de las matemáticas pueden expandir sus horizontes y profundizar en la comprensión de la teoría de números y la geometría analítica. En este artículo, vamos a profundizar en los conceptos clave que ampliarán tu mente sobre las potencias de la Unidad Imaginaria.
Definición y Propiedades Básicas
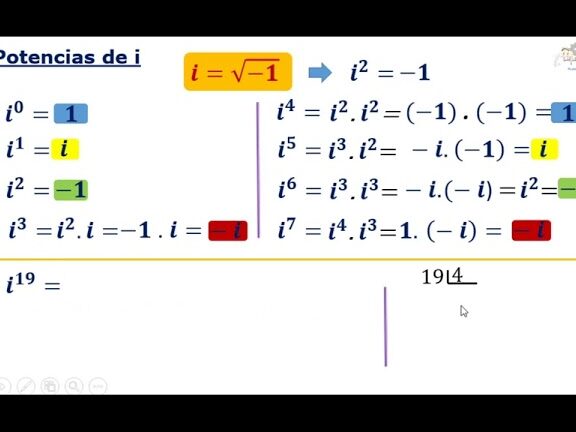
La Unidad Imaginaria, denotada como i, se define como la raíz cuadrada de -1. Esta unidad no se puede representar en la recta numérica real, por lo que se introduce un eje adicional, el eje imaginario, para representarla. Las propiedades básicas de la Unidad Imaginaria incluyen que i^2 = -1, i^3 = -i y i^4 = 1.
Operaciones con Números Complejos
Los números complejos se definen como la suma de un número real y un número imaginario, es decir, z = a + bi, donde a es el parte real y b es la parte imaginaria. Las operaciones con números complejos, como la suma y la multiplicación, se llevan a cabo utilizando las propiedades de la Unidad Imaginaria.
Principales Ríos de Europa: Lista Completa para EstudiarAplicaciones en la Física y la Ingeniería
Las potencias de la Unidad Imaginaria tienen un gran impacto en la resolución de problemas en la física y la ingeniería. Por ejemplo, en la teoría electromagnética, se utilizan números complejos para representar la amplitud y la fase de las ondas electromagnéticas. En la ingeniería eléctrica, se utilizan para analizar circuitos con componentes inductivos y capacitivos.
Relación con la Geometría Analítica
La Unidad Imaginaria también se relaciona con la geometría analítica, ya que permite la representación de figuras geométricas en el plano complejo. Esta representación permite analizar y resolver problemas geométricos de manera más eficiente y elegante.
Importancia en la Teoría de Números
La Unidad Imaginaria juega un papel crucial en la teoría de números, particularmente en la demostración del Último Teorema de Fermat. Esta demostración, hecha por Andrew Wiles en 1994, utilizó técnicas avanzadas de álgebra y análisis complejos, incluyendo la Unidad Imaginaria.
| Concepto | Definición |
|---|---|
| Unidad Imaginaria | La raíz cuadrada de -1, denotada como i. |
| Números Complejos | Suma de un número real y un número imaginario, z = a + bi. |
| Operaciones con Números Complejos | Suma y multiplicación de números complejos utilizando propiedades de la Unidad Imaginaria. |
| Aplicaciones en Física y Ingeniería | Representación de la amplitud y fase de ondas electromagnéticas, análisis de circuitos con componentes inductivos y capacitivos. |
| Relación con Geometría Analítica | Representación de figuras geométricas en el plano complejo, análisis y resolución de problemas geométricos. |
| Importancia en Teoría de Números | Demostración del Último Teorema de Fermat, técnicas avanzadas de álgebra y análisis complejos. |
Mas informacion
¿Qué son las potencias de la unidad imaginaria?
Las potencias de la unidad imaginaria son un concepto matemático fundamental en el ámbito de la teoría de los números y la teoría de Galois. Estas se definen como las potencias sucesivas de la unidad imaginaria, que se denota como i, es decir, i, i^2, i^3, i^4, etc. La unidad imaginaria i es un número complejo que satisface la relación i^2 = -1, lo que significa que no es un número real. Las potencias de la unidad imaginaria se utilizan en numerosas aplicaciones matemáticas y científicas, como la resolución de ecuaciones algebraicas, la teoría de la representación de grupos y la teoría de Galois, entre otras.
Profundizando en los Personajes de Romeo y Julieta¿Cómo se utilizan las potencias de la unidad imaginaria en la teoría de Galois?
En la teoría de Galois, las potencias de la unidad imaginaria se utilizan como elementos generadores de ciertos grupos de Galois. Un grupo de Galois es un grupo de automorfismos de un cuerpo que conserva la operación de suma y multiplicación. Las potencias de la unidad imaginaria se utilizan para construir extensiones galoisianas de cuerpos, que son extensiones algebraicas de cuerpos que son galoisianas. Estas extensiones se utilizan para resolver ecuaciones algebraicas y determinar si una ecuación algebraica dada es resoluble por radicales, es decir, si puede ser resuelta utilizando solo operaciones de suma, resta, multiplicación, división y raíces n-ésimas. Las potencias de la unidad imaginaria permiten la construcción de extensiones galoisianas que son cruciales para la resolución de este problema.
¿Qué relación hay entre las potencias de la unidad imaginaria y la resolución de ecuaciones algebraicas?
Las potencias de la unidad imaginaria están estrechamente relacionadas con la resolución de ecuaciones algebraicas. En particular, estas potencias se utilizan en la fórmula de Cardano para resolver ecuaciones cúbicas. Esta fórmula permite encontrar las raíces de una ecuación cúbica utilizando operaciones algebraicas y radicales, y las potencias de la unidad imaginaria juegan un papel clave en ella. De hecho, la fórmula de Cardano implica la utilización de la unidad imaginaria y sus potencias para reducir la ecuación cúbica a una ecuación cuadrática, que luego se puede resolver utilizando la fórmula cuadrática. Las potencias de la unidad imaginaria también se utilizan en la resolución de ecuaciones de grado superior, como ecuaciones de cuarto y quinto grado, y en la teoría de la resolubilidad de ecuaciones algebraicas.
¿Cómo se aplican las potencias de la unidad imaginaria en la teoría de la representación de grupos?
En la teoría de la representación de grupos, las potencias de la unidad imaginaria se utilizan como caracteres de representaciones de grupos. Un carácter de representación es una función que asigna a cada elemento de un grupo un número complejo, que satisface ciertas propiedades. Las potencias de la unidad imaginaria se utilizan como caracteres de representaciones irreducibles de grupos finitos, lo que permite la clasificación de estas representaciones. Esta clasificación es fundamental en la teoría de la representación de grupos, ya que permite entender la estructura interna de los grupos y sus acciones sobre espacios vectoriales. Las potencias de la unidad imaginaria también se utilizan en la teoría de la representación modular, que es una rama de la teoría de la representación de grupos que se ocupa de la representación de grupos finitos sobre cuerpos finitos.
Química en Acción: Orden, Distancia y Energía de EnlaceSi quieres conocer otros artículos parecidos a Potencias de la Unidad Imaginaria: Conceptos que Ampliarán tu Mente puedes visitar la categoría Lenguaje y Gramática.

Entradas relacionadas