Propiedades de los Números Combinatorios Explicadas
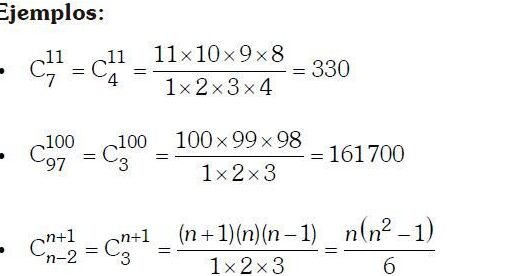
Los números combinatorios son una rama fascinante de la matemática, que se centra en el conteo y la enumeración de conjuntos. Estos números, también conocidos como números de combinación o combinatorios, han sido ampliamente utilizados en la resolución de problemas en álgebra, geometría, análisis, teoría de la probabilidad y teoría de grafos. A través de la combinatoria, los matemáticos han podido desarrollar técnicas para contar el número de maneras en que se puede seleccionar un subconjunto de un conjunto más grande, lo cual ha dado lugar a la creación de conceptos como el factorial y la combinatoria binomial. En este artículo, exploraremos las propiedades más interesantes de estos números y cómo se utilizan en la resolución de problemas matemáticos.
Propiedades de los Números Combinatorios Explicadas
Los números combinatorios son un concepto fundamental en la matemática, especialmente en la combinatoria y la teoría de grafos. Estos números se utilizan para contar el número de maneras en que se puede elegir o combinar objetos de un conjunto. A continuación, se presentan algunas de las propiedades más importantes de los números combinatorios.
Definición y Notación
Los números combinatorios se definen como el número de maneras en que se puede elegir k objetos de un conjunto de n objetos. Esta cantidad se denota como C(n, k) o n choose k. Por ejemplo, C(5, 3) indica que hay 10 maneras de elegir 3 objetos de un conjunto de 5.
Identidades Combinatorias
Existen varias identidades combinatorias importantes que se utilizan comúnmente en la resolución de problemas. Una de estas es la fórmula de Pascal, que establece que C(n, k) = C(n-1, k-1) + C(n-1, k). Esta fórmula se puede utilizar para construir el triángulo de Pascal, que es una forma visual de representar los números combinatorios.
Religión y Cultura de los Mayas: Resumen para Estudiar RápidoTriángulo de Pascal
El triángulo de Pascal es una representación visual de los números combinatorios. Cada fila del triángulo representa los valores de C(n, k) para un valor fijo de n, mientras que cada columna representa los valores de C(n, k) para un valor fijo de k. El triángulo de Pascal es una herramienta útil para visualizar y calcular los números combinatorios.
Aplicaciones en la Vida Real
Los números combinatorios se utilizan en una variedad de aplicaciones en la vida real, como la estadística, la teoría de grafos y la computación. Por ejemplo, en la estadística, los números combinatorios se utilizan para calcular la probabilidad de eventos. En la teoría de grafos, se utilizan para contar el número de caminos entre dos vértices en un grafo.
Relación con la Matemática Discreta
Los números combinatorios están estrechamente relacionados con la matemática discreta, que se ocupa del estudio de objetos matemáticos discretos, como enteros, grafo y álgebra booleana. La combinatoria, que es una rama de la matemática discreta, se basa en gran medida en los números combinatorios para contar y enumerar objetos.
| Concepto | Definición | Ejemplo |
|---|---|---|
| Definición y Notación | Los números combinatorios se definen como el número de maneras en que se puede elegir k objetos de un conjunto de n objetos. | C(5, 3) = 10 |
| Identidades Combinatorias | Existen varias identidades combinatorias importantes, como la fórmula de Pascal. | C(n, k) = C(n-1, k-1) + C(n-1, k) |
| Triángulo de Pascal | El triángulo de Pascal es una representación visual de los números combinatorios. | Triángulo de Pascal |
| Aplicaciones en la Vida Real | Los números combinatorios se utilizan en estadística, teoría de grafos y computación. | Probabilidad de eventos |
| Relación con la Matemática Discreta | Los números combinatorios están estrechamente relacionados con la matemática discreta. | Combinatoria y teoría de grafos |
Mas informacion
¿Qué son los números combinatorios?
Los números combinatorios son una rama de la matemática que se ocupa del estudio de los problemas de enumeración, es decir, la cuenta de las posibilidades de que algo ocurra. Estos números se utilizan en diversas áreas como la estadística, la teoría de la probabilidad, la combinatoria y la teoría de grafos. Los números combinatorios más comunes son los números de Pascal, que se utilizan para calcular la cantidad de maneras en que se puede elegir k elementos de un conjunto de n elementos. Estos números se presentan en forma de un triángulo, conocido como el triángulo de Pascal, que se caracteriza por tener un patrón de números que se repiten en diagonal.
Resumen Breve de "Las Soledades" de Góngora¿Cómo se utilizan los números combinatorios en la teoría de la probabilidad?
Los números combinatorios se utilizan en la teoría de la probabilidad para calcular la cantidad de maneras en que un evento puede ocurrir. Por ejemplo, si queremos saber la probabilidad de que salgan 3 caras al tirar 5 veces una moneda, necesitamos contar el número de maneras en que se puede elegir 3 caras de entre las 5 tiradas. Esta cuenta se hace utilizando los números combinatorios, que nos permiten calcular el número de maneras en que se puede elegir k elementos de un conjunto de n elementos. Luego, esta cuenta se divide entre el total de posibles resultados para obtener la probabilidad del evento.
¿Qué relación hay entre los números combinatorios y la estadística?
Los números combinatorios están estrechamente relacionados con la estadística, ya que se utilizan para calcular la cantidad de maneras en que se puede elegir k elementos de un conjunto de n elementos. En estadística, esta cuenta se utiliza para calcular la probabilidad de que un evento ocurra y para determinar la significación estadística de los resultados. Por ejemplo, en un experimento, si queremos saber la probabilidad de que salgan 3 caras al tirar 5 veces una moneda, necesitamos contar el número de maneras en que se puede elegir 3 caras de entre las 5 tiradas. Esta cuenta se hace utilizando los números combinatorios, que nos permiten calcular el número de maneras en que se puede elegir k elementos de un conjunto de n elementos. Luego, esta cuenta se divide entre el total de posibles resultados para obtener la probabilidad del evento.
¿Cómo se aplican los números combinatorios en la teoría de grafos?
Los números combinatorios se aplican en la teoría de grafos para contar el número de maneras en que se puede elegir k vértices de un grafo de n vértices. Por ejemplo, si queremos saber cuántas maneras hay de elegir 3 vértices de un grafo de 7 vértices, podemos utilizar los números combinatorios para calcular esta cuenta. Esta información es útil en la teoría de grafos para determinar la cantidad de subgrafos que se pueden formar con k vértices en un grafo de n vértices. Esta cuenta se hace utilizando la fórmula de combinatoria, que indica que el número de maneras de elegir k elementos de un conjunto de n elementos es C(n, k) = n! / (k!(n-k)! , donde C(n, k) es el número de maneras de elegir k elementos de un conjunto de n elementos, y ! indica factorial.
Resumen Esencial de la Leyenda de la LloronaSi quieres conocer otros artículos parecidos a Propiedades de los Números Combinatorios Explicadas puedes visitar la categoría Ciencia y Tecnología.

Entradas relacionadas